Copyright © 2005 by the author(s). Published here under licence by International Center for Tropical Agriculture (CIAT).
Latin America and the Caribbean (LAC) Population Database
We ask that users of this database acknowledge the source of the data with a reference to the following information:
Centro Internacional de Agricultura Tropical (CIAT), United Nations Environment Program (UNEP), Center for International Earth Science Information Network (CIESIN), Columbia University, and the World Bank (2005) Latin American and Caribbean Population Database. Version 3. Available from http://www.na.unep.net/datasets/datalist.php3 or http://gisweb.ciat.cgiar.org/population/dataset.htm
Contact: Glenn Hyman
Summary
The population of Latin America and the Caribbean increased from 175 million in 1950 to 515 million in 2000. Where did this growth occur? What is the magnitude of change in different places? How can we visualize the geographic dimensions of population change in Latin America and the Caribbean?
We compiled census and other public domain information to analyze both temporal and geographic changes in population in the region. Our database includes population totals for over 18,300 administrative districts within Latin America and the Caribbean. Tabular census data was linked to an administrative division map of the region and handled in a geographic information system. We transformed vector population maps to raster surfaces to make the digital maps comparable with other commonly available geographic information. Validation and error-checking analyses were carried out to compare the database with other sources of population information.
The digital population maps created in this project have been put in the public domain and can be downloaded from our website. The Latin America and Caribbean map is part of a larger multi-institutional effort to map population in developing countries. This is the third version of the Latin American and Caribbean population database and it contains new data from the 2000 round of censuses and new and improved accessibility surfaces for creating the raster maps.
Contents
- Introduction
- Part I: Boundary and population data
- Part II: Raster data
- References
- Download Data
- Appendices
- 1. Illustrative example of the stability of population estimates
- 2. LAC population database - summary table
- 3. Attribute item definitions
- 4. Country-specific documentation
- 5. Map of administrative units in LAC
- 6. Population density maps for 1960, 1970, 1980, 1990 and 2000
- 7. Roads used in the accessibility model
- 8. Populated places used in the accessibility model
- Acknowledgments
Introduction
The Latin America and Caribbean Population Database project contributes to a goal of several research and development organizations to provide digital population maps for the major developing-world regions. This project follows as closely as possible the design and methodology of previously-developed Asian and African databases (Deichmann 1994, Deichmann 1996a). The database has been updated since previous versions were published on the United Nations Environment Program's spatial data clearinghouse (UNEP 2000) and on CIAT’s web site. The new maps include new information from the 2000 census round for 16 countries. We improved the spatial resolution of the new map by collecting data at more detailed administrative levels for several countries, increasing the number of administrative units substantially compared to our previous release.
We include information on the sources of the population and administrative boundary data, procedures for compiling the data, and some indicators of the quality of the data set. Documentation of the methods to create the maps was derived from the earlier work for Africa and Asia. The raster population surfaces are based on a data set of over 18,300 administrative units and 10,700 populated places. Population growth rates were use to project population totals acquired at the date of each country census back to 1950 and forward to 2000. This documentation also includes appendices with information on data resolution and quality, data sources for population and administrative boundary information.
The main difference between this verison and previous efforts is that it includes a mechanism that incorporates new census and administrative data as they become available, and which ensures consistency with other sources and provides easy access to the data.
Part I: Boundary and population data
I.1. Discussion of data sources
The Latin America and Caribbean administrative boundaries and population database was compiled from medium-scale maps at country and sub-national level, national population censuses and United Nations data for the smaller islands of the Caribbean. Population data for all of mainland Latin America, Cuba, Puerto Rico, Jamaica, Trinidad and Tobago, Haiti and the Dominican Republic are from population census data. Most of the administrative boundary maps for mainland Latin America and the large Caribbean islands were digitized at the International Center for Tropical Agriculture (Jones and Bell 1997). Others were acquired from government agencies in the region. The smaller island nations of the Caribbean lack sub-national administrative units. The outlines of these countries are from the Digital Chart of the World. None of the input boundary or population data has been officially checked or endorsed by national statistical agencies, national geographic institutes or the United Nations.
Our work on this population mapping project progressed in parallel with the development of the Gridded Population of the World, Version 3, project (GPW3). The authors have all been involved in some aspects of GPW3 (CIESIN and CIAT, 2004). Much of the data checking for population figures was carried out in the context of the GPW3 project. Settlement points developed for GPW3 were used in the development of the accessibility model that is subsequently used to convert vector population maps to raster surfaces (CIESIN et al., 2004).
Boundaries
The scale of the source boundary maps vary from 1:50,000 to 1:1,125,000. Most of these boundaries were digitized during the 1990's from hard copy maps published in the 1980's and 1990's. In some cases, we acquired administrative division maps from national geographic institutes or from census bureaus. Users of the digital population maps should keep in mind the considerable differences in scale and quality of the input boundary maps. The quality of future boundary data should increase with improvements in capacity within the geographic and census institutes. Future efforts should rely on boundary information that is produced, verified and endorsed by the relevant agencies in each country. Appendix 4 includes more detailed information on the boundary data for each country used in the database.
In order to ensure a close match between different national maps, and to obtain maximum compatibility with other standard medium resolution data sets, all national boundaries and coastlines were replaced with the political boundaries template (PONET) of the Digital Chart of the World (DCW). The DCW is a set of basic digital GIS data layers with a nominal scale of 1:1 million scale. The use of a very detailed international boundaries template for, in some cases, relatively coarse resolution data is quite misleading, but was required to ensure a close match between the national maps. In any application, the smaller cartographic scale (i.e., coarser resolution) of the administrative boundary data in comparison to the international and coastlines template should be kept in mind.
For a few countries very detailed boundary data were available for which the spatial referencing information was not known. In light of the objectives of this project, these were nevertheless incorporated in order to achieve maximum resolution. Yet, the ad hoc transformation, projection change and rubbersheeting required to make these data compatible with the DCW template have no doubt introduced positional error which may well reach a magnitude in the order of 1-2 km.
Population data
With few exceptions, we used official census figures or official estimates, which were taken from national publications (census reports or statistical yearbooks) or from secondary data sources (yearbooks and gazetteers). The data was taken from censuses of the early 1990's or from more recent censuses near 2000. Several countries in the region have new data that is not yet publicly available. We expect to update our map when this new information becomes available. The specific sources of population data are indicated for each country in Appendix 4.
The accuracy of censuses varies by country. It was beyond the scope of this project to evaluate the accuracy of every census used, or of any of the official estimates. This would be possible since most censuses are followed by a post-census enumeration that provides an accuracy estimate. ECLAC, PRB and other sources giving country totals are likely to have values that are closer to the true value for the nation. The country totals have been corrected to account for inaccuracy in the census. Our data is from the original disaggregated censuses and does not incorporate these corrections. In countries that differed by more than 5 percent from the United Nations estimates (UN 2005), we made a uniform adjustment of the population data to bring it in line with the PRB country totals. In countries with functioning registration systems, population figures reach an accuracy within a fraction of a percent. In the US, census counts have been shown to have an accuracy of about 2 percent. With few exceptions, the accuracy of Latin American censuses is likely to be considerably lower.
Most countries in Latin America try to schedule their censuses at the beginning of a decade and at 10-year time intervals. The population data is generally from the 1990 or 2000 census rounds, with an average census date of 1996. In several cases our boundary data differed from the population data. The tabular population data listed more administrative units than were held in the boundary maps, a problem resulting from the creation of new municipal districts since the previous census. We handled this problem on a country-by-country basis by trying to find the discrepancies and then summing the data for municipal districts that had been subdivided.
I.2. Population projections and data quality
Estimation of population figures
Population projections were made on a country-by-country basis from the date of each census used to 1960, 1970, 1980, 1990 and 2000. Most of the projections were based on historical population growth rates for departments in Latin America and the Caribbean. The volume of papers and monographs on population projection methods in the demographic literature is very large. It is matched, however, by the number of publications that emphasize the continuing inability of these methods to accurately forecast population figures over more than very short time periods (O'Neill and Balk, 2001, also see the interesting discussion in Cohen, 1995).
For this project, we used ECLAC figures for population growth rates based on a mathematical trend forecast. In contrast to previous estimates for the global demography project, the current figures for each sub-national unit are based for most countries on a district-specific inter-censal growth rate between the last and the next to last enumeration. The inter-censal growth rate was calculated as
![Intercensal growth rate equation r = [ ln (p1/p2) ]/ t](images/figure-1.png)
where r is the average annual rate of growth, P1 and P2 are the population totals for two different time periods, and t is the number of years between the two enumerations (see, for example, Rogers 1985). The resulting growth rates were then used to derive estimates for the standard years. For example, based on enumerations in 1967 and 1977 and a corresponding rate r, the 1970 population would be calculated as:
![]()
In cases where no data were available for a year before 1960 or after 2000, the trend between the two closest enumerations was used to extrapolate the earliest or latest available data. Similarly, simple trend forecasts beyond 2000 could be made using the average growth rates between 1990 and 2000 as reflected in the figures in the GIS database.
For predictions over only a few years, mathematical trend projections are usually fairly accurate, and the specific type of function used has little influence on the results (Cohen 1995). A more elaborate estimation approach such as the cohort survival method would result in more reliable estimates, but the data requirements for this technique (age and sex distribution as well as age specific birth, death and migration rates) were far beyond what was possible in this project. Given the method used for the population forecasting, the characteristics of the available source data have a significant impact.
The population estimates are at best a rough estimate which should be interpreted within wide confidence margins. In general we can expect the reliability of the estimates to be lower, the longer the census upon which they are based lies back - that means the confidence intervals around the point estimates become increasingly wider over time. The data for some countries for which data were available for the early eighties only, need to be regarded as a best-guess only.
The figures included in the database are directly taken from the estimation and thus show more significant digits than is justified by their accuracy. During data manipulation and processing one should preserve all significant digits, but for presentation purposes, the figures should be rounded to reflect the uncertainty of the data. Even the use of population numbers to the nearest thousand in the above table is clearly optimistic.
Given the limited amount and quality of the base population data, we checked the resulting total national population figures against standard benchmarks, the regularly published population estimates produced by the UN. Obviously, the data are by themselves associated with a considerable amount of uncertainty since the estimates are based on conditional forecasts that make a number of assumptions regarding the most recent and future fertility, mortality and migration rates. They are also based, for the most part, on official census figures which sometimes prove to be highly unreliable. In cases where our estimate was considerably different from the UN estimate, the intercensal growth rates were adjusted uniformly such that the resulting estimate was equal to or close to the UN estimate (United Nations 1998). Typically this is the case where the latest available population figures were very old, or where a country experienced significant reductions in fertility in recent years that are not sufficiently reflected in the population dynamics between the last two censuses. The adjustments are indicated in the specific country documentation (Appendix I).
Several exceptions were made to our general use of the ECLAC population growth rate data to make population projections. In the case of the 16 countries where we had new 2000 census round data, projections for the last decade were calculated at the level of the available data - usually municipio level. We used ECLAC growth rate data to make projections for the larger islands -- Cuba, Jamaica, Puerto Rico, Trinidad and Tobago, Haiti and the Dominican Republic. The United Nations population projections (at the national level) were used for all the smaller Caribbean countries in our database where we lack sub-national boundary data (United Nations 1998). In a few additional cases we used national level population growth rates for the projections. United Nations population figures were used to calculate population growth rates in three cases:
- for Puerto Rico prior to 1990 where we had no information on population growth rates at sub-national levels;
- for Surinam and Guyana where census figures were available for only one point in time or the next to last census was too long ago, we applied the average annual national growth rate for a ten-year period centered on the target date. This modification resulted in a uniform adjustment of population figures across these two countries;
- for departments in Latin America with missing population growth rate data in the ECLAC database. This group included departments in Argentina (1), Brasil (2), Colombia (5), Cuba (1), Honduras (1), Mexico (1), Paraguay (4), and Venezuela (1).
Data quality estimates
Given our limited knowledge about the accuracy of the input data, it is impossible to make an objective assessment of data quality. The development of a qualitative index of boundary and population data quality was considered. However, such an index would be associated with considerable subjective judgment. Any question of "how good are the data?" is incomplete since we also have to ask "for what purpose?" Data that are clearly inappropriate for high resolution applications at the province or sub-province level, are still sufficiently accurate to be used in regional or continental scale applications (the prime motivation for this project), or for the visualization of spatial patterns in a country. Thus, we only provide some informal summary measures in the table below, and refer to the individual country documentation that provides all known details about the lineage of the data (admittedly, this knowledge is too often very limited). The user can consider this information to make his or her own decision about whether the data are appropriate for the specific tasks.
As in previous databases of this nature, we included two useful summary measures of data resolution in the summary table in the appendix:
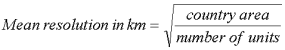
i.e. the length of a side of an administrative unit, if all units were square. And
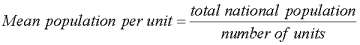
These two measures complement each other. In countries where large areas are uninhabitable, the mean resolution in km gives a biased impression of available detail. In such cases, the number of people per unit is a more meaningful indicator. The following table shows how these measures of resolution compare for Africa, Asia and Latin America.
| Continent | Mean resolution in km | Mean population per administrative unit ('000) |
|---|---|---|
| Asia | 117 | 1148 |
| Africa | 16 (32)1 | 7 (28)1 |
| Latin America and the Carribean | 33 | 29 |
1 Figures in parentheses indicate the values when South Africa (83,000 units) is discounted from the total of 109,268 units in Africa
There are 18,318 administrative units with population information in the data set. Much of the reduction of resolution in kilometers for Latin America and the Caribbean is due to the high level of detail for Brazil, with about one third of all the units for the data set. The population data for all the countries of Latin America was collected at a finer level of detail. The reduction in mean population per unit reflects the higher resolution in kilometers, and in comparison with Asia, lower population densities.
Part II: Raster data
The Latin America and Caribbean data set was prepared with similar design and methodology as that of the Africa and Asia data set previously developed (Deichmann 1994, Deichmann 1996a). The global demography project at NCGIA produced a gridded data set for the whole world which was constructed using a smoothing technique that has the property of preserving population totals within each administrative unit (Tobler et al. 1995). The raster surfaces based on the approach outlined in the following section were constructed using an alternative interpolation method. This method preserves population totals in each district as well and incorporates additional information on settlements, transport infrastructure and other features important in determining population distribution. The conversion of population data from a vector or polygon representation to raster format has the added advantage that the data can be more easily combined with many spatially referenced physical data sets which are most often stored in a gridded format. The raster format facilitates the use of these data in research and policy analysis and will hopefully contribute towards an increasingly integrated approach to the study of problems related to population, the environment, economics and culture as advocated, among others, by Cohen (1995). The approach outlined here as well as alternative approaches to spatial population modeling are discussed in more detail in Deichmann (1996b).
II.1. Gridding approach
The basic assumption upon which the construction of population distribution raster grids for Latin America and the Caribbean is based is that population densities are strongly correlated with accessibility. Accessibility is most generally defined as the relative opportunity of interaction and contact. These opportunities are the largest where people are concentrated and transport infrastructure is well developed. Within any given area, we therefore expect a larger share of the known total population to live in more accessible regions compared to areas that are less well connected to major urban centers.
Summary description of the method
The method for the development of population raster grids consists of the following steps. The most important input into the model is information about the transportation network consisting of roads, railroads and navigable rivers. The second main component is information on urban centers. Data on the location and size of as many towns and cities as can be identified are collected, and these settlements are linked to the transport network. This information is then used to compute a simple measure of accessibility for each node in the network. The measure is the so-called population potential which is the sum of the population of towns in the vicinity of the current node weighted by a function of distance, whereby network distances rather than straight-line distances are used. The following figure illustrates the computation of the accessibility index for a single node.
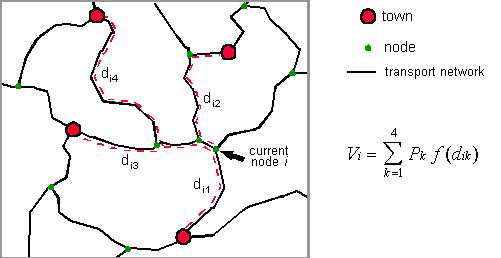
The computed accessibility estimates for each node are subsequently interpolated onto a regular raster surface. Raster data on inland water bodies (lakes and glaciers), protected areas and altitude are then used to adjust the accessibility surface heuristically. Finally, the population totals estimated for each administrative unit (as described in the first part of this documentation) are distributed in proportion to the accessibility index measures estimated for each grid cell. The resulting population counts in each pixel can then be converted to densities for further analysis and mapping. Each of these steps will now be described in more detail.
Construction of the transportation network
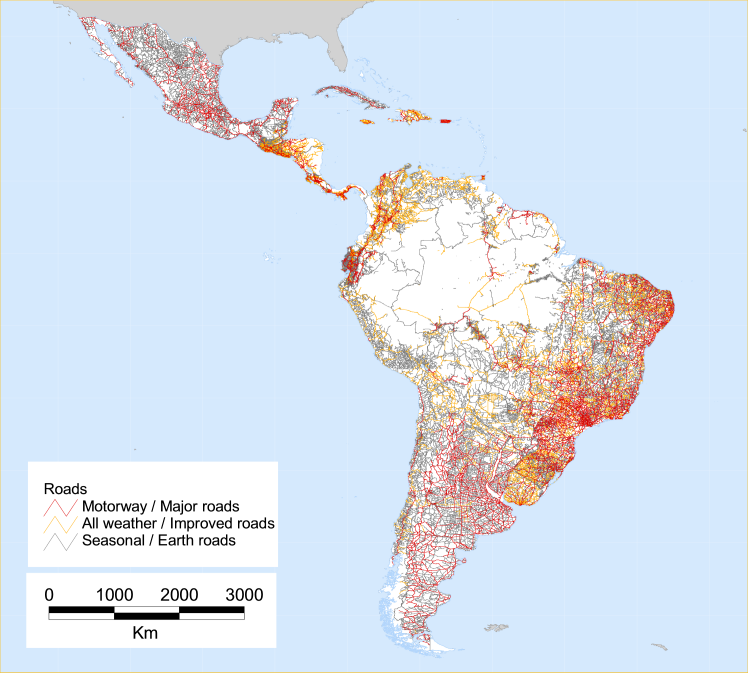
There are few data sources that provide consistent, geographically referenced base data layers for large areas such as an entire continent. The transportation infrastructure data for this project was constructed using the following data sets: roads and railways from the Digital Chart of the World (DCW) and major navigable waterways from the World Boundary Databank II (WBDII). WBDII originated at the U.S. Central Intelligence Agency and an Arc/Info version is available from the Environmental Systems Research Institute (ESRI). The nominal scale of WBDII is 1:3 million. The scale of the DCW base maps (the Operational Navigational Charts) is 1:1 million. Since we also used DCW for the international boundaries in the administrative unit data layers and since WBDII and DCW appear to share common ancestors, a good fit exists between the individual data layers.
The road dataset was improved by including road type characteristics from a range of paper and digital maps. Roads were identified as follows.
| Road type | Total length in km (and as a % of all roads) | Estimated travel speed (kmph) |
|---|---|---|
| Primary (Motorway/Major road) | 304,500 (22%) | 60 |
| Secondary (All weather/Improved) | 300,000 (21%) | 35 |
| Tertiary (Partially improved/Earth roads) | 802,000 (57%) | 25 |
| Other network types | ||
| Railroads | 120,000 | 40 |
| Navigable rivers | 265,000 | 10 |
| Auxillary arcs | 1,690,000 | 5 |
A brief technical discussion is now required to clarify the structure of the transportation data. After merging the individual components of the transport network into one data layer there are still no connections between the individual components (e.g., roads and rivers). To allow the model to choose the most efficient means of transport at any point in the network, the intersections between the individual transport layers need to be found. This is a standard GIS operation that results in a well-structured data layer of arcs (or links) representing roads or rivers. These are connected by nodes which are intersections of two or more arcs of different or similar types. Nodes, of course also represent the end of an unconnected arc.
The program used for calculating accessibility produces an estimate for each node in the network. The problem in an application where the network is sparse in many regions is that no values are derived for areas that are not connected to the network. Also, DCW only includes fairly important transport features that are relevant at a cartographic scale of 1:1 or 1:3 million. One solution is to calculate the accessibility index for the center of each grid cell of the subsequently generated output raster. From each grid cell, the distance to the closest transport feature could be calculated and added to the network distances to the closest towns. This approach was used by Geertman and van Eck (1995).
However, this approach is not realistic where the closest access point to the transport network is at a location which is actually far away from urban centers. Another network access location may be further away from the grid cell initially, but better connected to major towns. To evaluate different options of network access for each grid cell would be impractical, and we therefore chose a different approach. In areas where the transport network is sparse, auxiliary arcs were added which could be thought of as "feeder roads". Essentially, this implies that people who may be living in these remote areas are using trails or tracks to get to the main transport network first and then continue their travel to the nearest city along the fastest routes. The algorithm automatically determines which network access is optimal in minimizing overall travel times.
It would be straightforward to use simple network distance for the calculation of accessibility. However, different arcs representing various transportation modes are associated with quite different travel speeds. For example, a kilometer travel on a paved road will take much less time than the same distance on a river. Instead of simple distance, we therefore used cumulative travel time as the weight in the accessibility calculation. Each arc in the resulting complete transportation network is associated with an estimate of average travel speed that is thought to be possible. Primary roads were assumed to allow for a travel time of 60kmph, secondary roads were assigned a speed of 35kmph, and tertiary roads were assigned a speed of 25kmph. 40kmph were used for railroads, 10kmph for navigable rivers, and 5kmph for the auxiliary network access routes. For each arc, we calculated the real-world distance in kilometers.
All data layers are referenced in geographic (latitude/longitude) coordinates and no map projection is able to represent real-world distances in all directions with sufficient accuracy for large regions. We therefore calculated the correct length of each arc as the sum of the great-circle distances of all individual segments that make up the arc between two nodes. The time it takes to traverse each section of the transport network is then simply its length in km divided by the travel speed associated with the specific mode of transport.
Setting up urban data
The accessibility index is the sum of the population totals of the towns in the vicinity of the current location weighted by the network travel time ("distance") to those towns. Data on the location and size of urban centers were provided by CIESIN and accounted for 10,700 cities with population estimates for year 2000.
Towns need to be connected to the transport network to enable the accessibility calculation algorithm to find the closest towns for each node in the network. Each settlement was therefore assigned to the network node closest to its recorded location.
Run accessibility calculation
For the actual accessibility calculation we used a stand-alone program written in the C programming language. This program reads the entire network definition which consists of (a) the identifiers for each node and the population size of the town that corresponds to the node - zero in most cases, indicating that no town is located at the node -, and (b) the identifiers of the two nodes that define each arc and the travel time required to traverse the arc.
A further option of the program that allows for considering the direction of travel along an arc was not used. This implies that there are no "one-way streets" and that travel time is the same regardless of which way one travels. This assumption could be relaxed since, for example, travel speeds are lower up-river than down-river, but the added gain in realism will not compensate for the additional effort required in defining these details. Also, no further assumptions are made about modal choice. In moving through the network, an imaginary traveler may change his or her means of transport at will. This is unrealistic since a switch, say from road travel to a train and on to a boat, are all associated with delays. Even so, in order to keep the model simple (and run-times manageable) we did not introduce a penalty for switching the transport mode. A modification relevant to an application in a regional setting was made, however. For any arc that crosses an international boundary, the travel time was increased by 30 minutes reflecting delays in border crossings. This added travel time could be varied depending on the relations between two neighboring countries. This would either require subjective judgment or very detailed information on the permeability of international borders.
For each node in the network, the program now finds the network path to each of a specified number of towns that results in the lowest overall travel time. In the initial program specification, all towns reached within a user-defined specified travel time (e.g., 5 hours) were determined. However, in areas where towns are sparsely distributed and the number of nodes and arcs is large, this resulted in unacceptably long run-times. Instead, we modified the program to find the closest four towns or less if fewer than four towns were accessible within a more generous threshold travel time. This also makes the index somewhat more comparable across large areas, since the previous specification resulted in the accessibility index for some densely urbanized areas to be based on fifty or more towns, while other regions would only contain two or three.
For the shortest path calculation the program uses the standard Dijkstra algorithm. The program section used for this search consists of a modified version of a fast implementation of this algorithm developed by Tom Cova, a transportation GIS specialist at NCGIA. The Dijkstra algorithm evaluates the network structure around the current location starting from the center and reaching out further and further. For applications in which only one origin-destination pair is of interest, this is inefficient and various modifications have been suggested to speed up the search. In this application, in contrast, the interest is in finding the shortest path to all towns within the vicinity and the Dikstra's "shortcoming" is actually a bonus. The slightly modified algorithm thus "collects" towns as it ventures out from the originating node. Once four towns have been found and the program has determined that all additional connected arcs will not lead to a town that is closer than those already found, the search is terminated and the town populations and travel times are passed to a program section that calculates the accessibility measure.
This measure is the sum of the town populations weighted by a negative exponential function of travel time ("distance"), i.e.
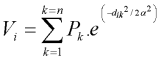
where Vi is the accessibility estimate for node i, Pk is the population of town k, dik is the travel time/distance between node i and town k, and is the distance to the point of inflection in the distance decay function. This parameter was set to one hour in this case which means that the influence of a town one hour away decreases to about 60 percent, and a town two hours away will only contribute 14 percent of its total population to the accessibility index. Rather than using total urban population, we applied a square root transformation to the population figures, implying that each additional person living in a city has an increasingly lower influence. This transformation avoids an exaggerated influence of very large mega-cities while being less of an equalizer than the more common log-transformation.
Interpolation
The accessibility index that is available for each of the nodes in the network needs to be converted into a regular raster grid. We used a simple inverse distance interpolation procedure that resulted in a relatively smooth surface. A problem with this technique is that interpolated values will not fall outside the range of the values recorded at the neighboring node locations. In analogy to interpolating elevation data: if recorded values are available only for locations on the slope of a mountain but not at the peak, the interpolated value for the summit location will be underestimated. Conversely in our application, if values are recorded only for network nodes, but not for areas that are remote from transport routes (e.g., deserts), then using the neighboring node values for interpolation will overestimate the accessibility for the remote location.
Yet, experiments with other interpolation procedures did not result in satisfactory results. Thin plate spline interpolation may be more appealing theoretically since it would allow values at interpolated locations to fall below (or above) those that are recorded at neighboring locations if the overall tension surface suggests a corresponding trend. However, the values estimated for some locations were clearly out of the range of what would be reasonable. Given the large number of nodes introduced in remote areas by adding the auxiliary access routes, we considerthe simple inverse distance interpolation to be sufficiently accurate.
Adjustment of the accessibility measure
Three additional data sets were used to adjust the resulting accessibility index grid: inland water bodies, protected areas, and elevation. Lake areas were masked and grid cells that fell onto a glacier were assigned an accessibility value of zero. This information was derived from the DCW lakes layer.
GIS data layers on protected areas were obtained from the World Conservation Monitoring Center (WCMC). Unfortunately, little information about each protected area was available besides its name, such that it was impossible to relate, for example, protection status to an estimate of how much the areas may still be used and inhabited by people. We reduced the accessibility index for grid cells that fell into national parks to 20 percent of the original value. These values are subjectively determined to allow for the fact that the protection of protected areas is not always perfect. Since most of these parks are in remote region, the change in predicted population densities that would be introduced by varying the adjustment factors should be small.
Areas higher than 5000 m were masked out of the analysis. Many of these areas in the Andes lack protected area status, but are uninhabited. We made no adjustment to areas below 2000 m. Between 2000 and 5000 m we weighted the accessibility measure with higher areas having less accessibility. Several major cities in the Andes are above 2000 meters but at increasingly higher elevations population density markedly drops.
Distribution of population
The distribution of the population total available for each administrative unit over the grid cells that fall into that unit is straightforward. The accessibility values estimated for each grid cell serve as weights to distribute population proportionately. First the grid cells in the accessibility index are summed within each district. Each value is divided by the corresponding district sum such that the resulting weights sum to one within each administrative unit. Multiplying each cell value by the total population yields the estimated number of people residing in each grid cell. The standardization of the accessibility index implies that the absolute magnitudes of the predicted access values are unimportant - only the variation within the administrative unit determines population densities within each district.
Again, we have to take account of the fact that all GIS data layers and raster grids are referenced in latitude/longitude coordinates. This means that grid cells further away from the equator represent a smaller real-world area than grid cells close to it. For example, a 2.5 minute grid cell has a real-world area of 10.8 square km at 60 degrees latitude, of 18.6 square km at 30 degrees and of 21.4 square km at the equator. We therefore weighted the accessibility index value for each grid cell by the actual area of the grid cell before standardizing the values within each district.
Because only the relative magnitudes of the accessibility index are important in distributing total population, and since most administrative units are fairly small, the error introduced by the distortions of the geographic coordinate system will usually be insignificant. However, in areas where the available resolution of the administrative units is fairly low, the difference in the actual areas of grid cells within a district that are located further away from the equator compared to those closer to the equator can be relatively large. For example, in LAC which reaches into much higher latitudes than Africa, the resulting difference in predicted population densities using undadjusted and adjusted accessibility values reached up to eight people per square km. From the grid cells of total population, population density images are created by dividing the population counts estimated for each grid cell by the real-world area in square km of that cell.
Evaluating the accuracy of this interpolation method is difficult in the absence of very high resolution population data (e.g., by enumeration areas) that could be used as a benchmark. For the Asian database a simple experiment was conducted in which state level population figures for India were interpolated. The total population allocated to each district could then be compared to the actual district figures. The differences are acceptable in relatively homogeneous regions but are obviously quite large in areas where population distribution is very scattered such as in high mountain or desert regions. The same results could be expected for Africa. The model will work better, the more detailed the administrative data, the more urban population figures are available, and the more homogeneous the population is distributed.
References
American Association for the Advancement of Science. (2002) AAAS Atlas of Population and Environment. http://atlas.aaas.org/.
Bongaarts, J. (1996) Population pressure and the food supply system in the developing world. Population and Development Review. 22(3)483-503.
Brockerhoff. (2000) An urbanizing world. Population Bulletin. Washington DC. Population Reference Bureau. 55(3).
Browder, J. O. And B. J. Godfrey. (1997) Rainforest Cities: Urbanization, Development, and Globalization of the Brazilian Amazonia. New York: Columbia University Press.
CELADE (Centro Latinoamericano y Caribeño de Demografía). (2001) Urbanización y evolución de la población urbana de America Latina, 1950-1990. Boletín Demográfico. Santiago de Chile, año 33, No. Especial, base de datos DEPUALC.
Center for International Earth Science Information Network (CIESIN), Columbia University; and Centro Internacional de Agricultura Tropical (CIAT), (2004) Gridded Population of the World (GPW), Version 3. Palisades, NY: Columbia University. Available at http://beta.sedac.ciesin.columbia.edu/gpw.
Center for International Earth Science Information Network (CIESIN), Columbia University; International Food Policy Research Institute (IPFRI), the World Bank; and Centro Internacional de Agricultura Tropical (CIAT), (2004) Global Rural-Urban Mapping Project (GRUMP): Settlement Points. Palisades, NY: CIESIN, Columbia University. Available at: http://beta.sedac.ciesin.columbia.edu/gpw
Center for International Earth Science Information Network (CIESIN), Columbia University; International Food Policy Research Institute (IPFRI), the World Bank; and Centro Internacional de Agricultura Tropical (CIAT), (2004) Global Rural-Urban Mapping Project (GRUMP): Urban Extents. Palisades, NY: CIESIN, Columbia University. Available at: http://beta.sedac.ciesin.columbia.edu/gpw
Center for International Earth Science Information Network (CIESIN), Columbia University; International Food Policy Research Institute (IPFRI), the World Bank; and Centro Internacional de Agricultura Tropical (CIAT), (2004) Global Rural-Urban Mapping Project (GRUMP): Gridded Population of the World, version 3, with Urban Reallocation (GPW-UR). Palisades, NY: CIESIN, Columbia University. Available at: http://beta.sedac.ciesin.columbia.edu/gpw
CEPAL (Comisión Económica para América Latina). (2000). Distribución Espacial y Urbanización en América Latina y El Caribe (DEPUALC). Base de datos, Espina, R. (2000), LC/R 1999. Santiago, Chile.
Cincotta, R., J Wisnewski and R. Engelman. (2000). Human population in the biodiversity hotspots. Nature. 404:990-992.
Cohen, J. (1995), How many people can the Earth support?, Norton, New York.
Cuffaro, N. (1997). Population growth and agriculture in poor countries: a review of theoretical issues and empirical evidence. World Development. 25(7):1151-1163.
Defense Mapping Agency. (1994). Digital Chart of the World, digital data, 1:1 mio sclae, Arc/Info version produced by Environmental Systems Research Instititue.
Deichmann, U. and L. Eklundh (1991). Global digital datasets for land degradation studies: A GIS approach, GRID Case Study Series No. 4, Global Resource Information Database, United Nations Environment Programme, Nairobi.
Deichmann, U. (1994). A medium resolution population database for Africa, Database documentation and digital database, National Center for Geographic Information and Analysis, University of California, Santa Barbara.
Deichmann, U. (1996a). Asia medium resolution population database documentation, Database documentation and digital database prepared in collaboration with UNEP/GRID Geneva for the UNEP/CGIAR Initiative on Use of GIS in Agricultural Research, National Center for Geographic Information and Analysis, University of California, Santa Barbara.
Deichmann, U. (1996b). A review of spatial population database design and modeling, paper prepared for the UNEP/CGIAR Initiative on the Use of GIS in Agricultural Research, National Center for Geographic Information and Analysis, Santa Barbara.
Dijkstra, E.W. (1959). A note on two problems in connexion with graphs, Numerische Mathematik, 1, 269-271.
Dobson, J., E. Bright, P. Coleman, R. Durfee and B. Worley. (2000). Landscan: a global population database for estimating populations at risk. Photogrammetric Engineering and Remote Sensing. 66(7):849-857.
Geertman, S.C.M. and J.R. Ritsema van Eck (1995). GIS and models of accessibility potential: an application in planning, International Journal of Geographic Information Systems. 1:67-80.
Global Environment Facility. (2002). The Challenge of Sustainability: An Action Agenda for the Global Environment. http://gefweb.org/Outreach/outreach-PUblications/MainBook.pdf.
Guzman, J., S. Singh, G. Rodriguez and E. Pantelides. Editors. (1996). The Fertility Transition in Latin America. Oxford: Clarendon Press.
Jones, P.G. and W. C. Bell (1997). Administrative Divisions of Latin America to the Third Order, Digital Version 1.1. CIAT Cali-Colombia.
Livernash, R. and E. Rodenburg. (1998). Population change, resources and the environment. Population Bulletin. Washington DC. Population Reference Bureau. 53(1).
Lonergran, S. (1998). The role of environmental degradation in population displacement. Research Report No. 1. Global Environmental Change and Human Security Project. International Human Dimensions Programme on Global Environmental Change.
Loveland, T.R., Reed, B.C., Brown, J.F., Ohlen, D.O., Zhu, J, Yang, L., and Merchant, J.W., (2000). Development of a Global Land Cover Characteristics Database and IGBP DISCover from 1-km AVHRR Data. International Journal of Remote Sensing, v. 21, no. 6/7, p. 1,303-1,330.
Loveland, T.R., Estes, J.E., and Scepan, J., (1999). Introduction: Special Issue on Global Land Cover Mapping and Validation. Photogrammetric Engineering and Remote Sensing, v. 65, no. 9, p. 1011-1012.
Lutz, W., W. Sanderson and S. Scherbov. (2001). The end of world population growth. Nature. 412:543-545.
Martin, P. and J. Widgren. (1996). International migration: a global challenge. Population Bulletin. Population Reference Bureau. Washington DC. 51(1).
Merrick, Thomas. (1991). Population pressures in Latin America. Population Bulletin. Population Reference Bureau. Washington DC. 41(3).
O'Neill, Brian and Deborah Balk. (2001). Projecting Future World Population. Population Bulletin. Population Reference Bureau. Washington DC. 56(3).
Population Division of the United Nations Secretariat. (1998). United Nations world population projection to 2150. Population and Development Review. 24(1)183-189.
Simoneau, K. (1990). South American Population Censuses Since Independence: An Annotated Bibliography of Secondary Sources. Seminar on the Acquisition of Latin American Library Materials. University of Wisconsin-Madison. Madison, Wisconsin (HB3558 S56).
Rogers, A. (1985). Regional population projection models, Sage, Beverly Hills.
Tobler, W., U. Deichmann, J. Gottsegen and K. Maloy (1995). The global demography project, Technical Report 95-6, NCGIA, Santa Barbara.
United Nations (1998), Principles and recommendations for population and housing censuses, revision 1, Department for Economic and Social Information and Policy Analysis, Statistics Division, New York.
United Nations (2005), World population prospects. The 2004 revision, Department for Economic and Social Information and Policy Analysis, Statistics Division, New York.
United Nations (2003), World urbanization prospects. The 2003 revision, Department for Economic and Social Information and Policy Analysis, Statistics Division, New York.
U.S. Bureau of the Census (2004), Countries of the World - Census dates, International Programs Center, Population Division, Washington, D.C.
United Nations Environment Program. (2000. Latin America and Caribbean Population Database Documentation. On-line at UNEP North America website: http://grid2.cr.usgs.gov/globalpop/lac/intro.html/
Van Lindert, P. and O. Verkoren. Editors. (1997). Small Towns and Beyond: Rural Transformation and Small Urban Centres in Latin America. Amsterdam: Thela Publishers.
Appendices
A.1. Illustrative example of the stability of population estimates
For Israel, population figures were available for a number of years in the Statistical Yearbook of Israel 1991. The following table shows the total population for the six districts of Israel for four recent years. The last three columns show total population estimates for 1995 based on average annual growth rates between each of the first four years and 1990. The choice of the growth rate obviously has a considerable effect on the resulting estimate. Even allowing for the special nature of Israel's population dynamics due to the country's immigration policy (the most likely explanation for the high 1989-90 rates), the fact that the estimates are strongly dependent on the available input data becomes clear.
| District | Total population (`000)1 | Average annual percentage growth rate | Resulting estimates (`000) for 1995 based on rate for | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1985 | 1987 | 1989 | 1990 | 85-90 | 87-90 | 89-90 | 85-90 | 87-90 | 89-90 | |
| Jerusalem | 506 | 533 | 556 | 578 | 2.66 | 2.70 | 3.88 | 660 | 662 | 702 |
| Northern | 707 | 732 | 763 | 805 | 2.60 | 3.17 | 5.36 | 917 | 943 | 1052 |
| Haifa | 593 | 601 | 613 | 656 | 2.02 | 2.92 | 6.78 | 726 | 759 | 921 |
| Central | 889 | 928 | 970 | 1032 | 2.98 | 3.54 | 6.20 | 1198 | 1232 | 1407 |
| Tel Aviv | 1015 | 1027 | 1044 | 1095 | 1.52 | 2.14 | 4.77 | 1181 | 1218 | 1390 |
| Southern | 511 | 526 | 542 | 574 | 2.33 | 2.91 | 5.74 | 645 | 664 | 765 |
1 Data Source: Central Bureau of Statistics (1991), Statistical Abstract of Israel 1991, Jerusalem.
A.2. LAC population database - Summary table*
| Region | Area (km2) | Number of units | Mean resolution in km | Number of people per unit1 | Pop. 19602 | Pop. 19702 | Pop. 19802 | Pop. 19902 | Pop. 20002 |
|---|---|---|---|---|---|---|---|---|---|
| LAC | 20,469,646 | 18317 | 33 | 29 | 218,575 | 285,194 | 362,209 | 443,749 | 522,928 |
| North America | 1,962,007 | 2415 | 29 | 41 | 36,940 | 50,611 | 68,046 | 84,296 | 100,088 |
| Caribbean | 234,222 | 393 | 24 | 95 | 20,425 | 24,832 | 29,216 | 33,824 | 37,457 |
| Central America | 517,692 | 4584 | 11 | 8 | 12,781 | 17,286 | 22,673 | 28,504 | 35,950 |
| South America | 17,755,725 | 10925 | 40 | 32 | 148,429 | 192,465 | 242,274 | 297,125 | 349,433 |
| Country | Area (km2) | ISO code | Number of units | Mean resolution in km | Number of people per unit1 | Pop. 19602 | Pop. 19702 | Pop. 19802 | Pop. 19902 | Pop. 20002 |
|---|---|---|---|---|---|---|---|---|---|---|
| Aruba | 189 | ABW | 1 | 14 | 92 | 49 | 57 | 60 | 66 | 92 |
| Anguilla | 83 | AIA | 1 | 9 | 11 | 6 | 7 | 7 | 9 | 11 |
| Netherlands Antilles | 736 | ANT | 2 | 19 | 88 | 135 | 159 | 174 | 191 | 176 |
| Argentina | 2779454 | ARG | 499 | 75 | 74 | 20616 | 23962 | 28094 | 32581 | 36896 |
| Antigua And Barbuda | 444 | ATG | 2 | 15 | 38 | 55 | 66 | 63 | 63 | 76 |
| Bahamas | 13362 | BHS | 16 | 29 | 19 | 110 | 170 | 210 | 255 | 301 |
| Belize | 22290 | BLZ | 6 | 61 | 40 | 93 | 123 | 144 | 186 | 242 |
| Bolivia | 1087732 | BOL | 100 | 104 | 83 | 3351 | 4212 | 5355 | 6669 | 8317 |
| Brasil | 8518834 | BRA | 5508 | 39 | 32 | 72742 | 95989 | 121615 | 149394 | 173858 |
| Barbados | 441 | BRB | 1 | 21 | 266 | 231 | 239 | 249 | 257 | 266 |
| Chile | 750612 | CHL | 290 | 51 | 53 | 7643 | 9570 | 11174 | 13179 | 15412 |
| Colombia | 1142845 | COL | 1069 | 33 | 39 | 16857 | 22561 | 28447 | 34970 | 42120 |
| Costa Rica | 51381 | CRI | 82 | 25 | 48 | 1334 | 1821 | 2347 | 3076 | 3929 |
| Cuba | 111634 | CUB | 169 | 26 | 66 | 6976 | 8483 | 9645 | 10537 | 11125 |
| Cayman Islands | 279 | CYM | 3 | 10 | 13 | 9 | 10 | 17 | 26 | 40 |
| Dominica | 769 | DMA | 10 | 9 | 8 | 60 | 71 | 74 | 72 | 78 |
| Domincan Republic | 48351 | DOM | 30 | 40 | 276 | 3231 | 4424 | 5718 | 7090 | 8265 |
| Ecuador | 247399 | ECU | 956 | 16 | 13 | 4439 | 5970 | 7961 | 10272 | 12306 |
| Guadeloupe | 1797 | GLP | 11 | 13 | 39 | 275 | 320 | 327 | 391 | 430 |
| Grenada | 325 | GRD | 1 | 18 | 102 | 90 | 94 | 90 | 96 | 102 |
| Guatemala | 108705 | GTM | 329 | 18 | 34 | 4139 | 5418 | 7012 | 8894 | 11166 |
| French Guyana | 83634 | GUF | 21 | 63 | 8 | 32 | 48 | 68 | 116 | 164 |
| Guyana | 211244 | GUY | 10 | 145 | 74 | 569 | 709 | 761 | 729 | 744 |
| Honduras | 111911 | HND | 3693 | 6 | 2 | 1894 | 2592 | 3568 | 4867 | 6424 |
| Haiti | 26876 | HTI | 10 | 52 | 794 | 3803 | 4520 | 5453 | 6867 | 7939 |
| Jamaica | 11060 | JAM | 14 | 28 | 185 | 1629 | 1869 | 2133 | 2369 | 2585 |
| Saint Kitts and Nevis | 277 | KNA | 2 | 12 | 20 | 51 | 45 | 43 | 41 | 40 |
| St. Lucia | 620 | LCA | 1 | 25 | 154 | 90 | 104 | 118 | 138 | 154 |
| Mexico | 1962007 | MEX | 2415 | 29 | 41 | 36940 | 50611 | 68046 | 84296 | 100088 |
| Montserrat | 103 | MSR | 1 | 10 | 4 | 12 | 12 | 12 | 11 | 4 |
| Martinique | 1146 | MTQ | 1 | 34 | 386 | 282 | 325 | 326 | 360 | 386 |
| Nicaragua | 127976 | NIC | 144 | 30 | 34 | 1617 | 2228 | 3067 | 3960 | 4959 |
| Panama | 74974 | PAN | 67 | 33 | 44 | 1126 | 1506 | 1949 | 2411 | 2950 |
| Peru | 1297712 | PER | 1895 | 26 | 14 | 9931 | 13193 | 17324 | 21753 | 25952 |
| Puerto Rico | 8985 | PRI | 78 | 11 | 49 | 2360 | 2716 | 3197 | 3528 | 3835 |
| Paraguay | 400339 | PRY | 228 | 42 | 24 | 1842 | 2350 | 3114 | 4219 | 5470 |
| El Salvador | 20455 | SLV | 263 | 9 | 24 | 2578 | 3598 | 4586 | 5110 | 6280 |
| Surinam | 146755 | SUR | 10 | 121 | 43 | 290 | 372 | 356 | 402 | 434 |
| Turks And Caicos | 548 | TCA | 1 | 23 | 19 | 6 | 6 | 8 | 12 | 19 |
| Trinidad and Tobago | 5202 | TTO | 30 | 13 | 43 | 843 | 971 | 1082 | 1215 | 1285 |
| Uruguay | 177038 | URY | 19 | 97 | 176 | 2538 | 2808 | 2914 | 3106 | 3342 |
| St. Vincent | 453 | VCT | 1 | 21 | 116 | 81 | 90 | 100 | 109 | 116 |
| Venezuela | 912128 | VEN | 320 | 53 | 76 | 7579 | 10721 | 15091 | 19735 | 24418 |
| British Virgin Islands | 166 | VGB | 4 | 6 | 5 | 8 | 10 | 11 | 17 | 21 |
| U.S. Virgin Islands | 374 | VIR | 3 | 11 | 37 | 33 | 64 | 99 | 104 | 111 |
1 Population figures given in thousands for year 2000
2 Estimates (in thousands) from World Population Prospects: The 2004 Revision, as of March 2005.
A.3. Attribute item definitions
| Polygon Attribute Table | ||
|---|---|---|
| Position | Item | Description |
| 17 | SQKM | Area of the polygon |
| 21 | ADMSQKM | Area of the admin unit (sum of SQKM) |
| 25 | CODE | L-Land, IS-Island, IW-Inland Waterbody |
| 28 | ADMINID | Administrative Unit ID (see below) |
| 32 | COUNTRY | 3-Letter ISO Country ID |
| 35 | NAME1 | Name of first subnational level unit |
| 60 | NAME2 | Name of second subnational level unit ('N.A.' if not available) |
| 85 | NAME3 | Name of third subnational level unit ('N.A.' if not available) |
| 110 | NAME4 | Name of fourth subnational level unit ('N.A.' if not available) |
| 135 | NAME5 | Name of fifth subnational level unit ('N.A.' if not available) |
| 160 | DEMOFLAG | 1 for the major polygon belonging to the admin unit, 0 elsewhere (see below) |
| 162 | P60 | Total estimated population 1960 |
| 166 | P70 | Total estimated population 1970 |
| 170 | P80 | Total estimated population 1980 |
| 174 | P90 | Total estimated population 1990 |
| 180 | P00 | Total estimated population 2000 |
| Arc Attribute Table | ||
| 29 | FEATURE | 0 - International Boundary 1 - Boundary of first level unit 2 - Boundary of second level unit 3 - Boundary of third level unit 9 - Boundary with "outside polygon" |
ADMINID - consisting of
3-digit UN country code + 2-digit first level unit code + 2-digit second
level unit code + 2-digit third level unit code + 2-digit fourth level unit
code + 2-digit fifth level unit code.
To produce the subnational code, the administrative units were (a) sequentially numbered based on a list of administrativeunits in an official census publication if available, or (b) alphabetically ordered otherwise.
DEMOFLAG - indicates the major (i.e., biggest) polygon in cases where an administrative unit consists of more than one polygon. For all polygons belonging to the same unit, the full attribute information is replicated in the data table. Therefore, for any frequency table construction or summary statistics calculation, one needs to select the polygons with a FLAG value of one first to avoid double counting.
A.4. Country-specific documentation
Notes
For countries that are not featured in the list below:
- The source for the spatial data is DCW.
- The source for the population data is the UN World Population Prospects: 2004 Revision.
Argentina
| Spatial data | Population data |
|---|---|
| Atlas de Suelos de la República Argentina. Inta y la Fundación Argentina. | Provincia segun departamento. Poblacion censada en 1991 y 2001 y variacion intercensal aboluta y ralativa 1991-2001. Censo Nacional de Poblacion, Hogares y Viviendas del ano 2001. Instituto Nacional de Estadistica Y Censos Argentina. http://www.indec.mecon.ar/webcenso/index.asp |
Belize
| Spatial data | Population data |
|---|---|
| Mapa de la Regionalización de la República de Guatemala. Ministerio de Agricultura. Escala 1:750000. Copia heliográfica. | Central Statistical Office, Ministry of Finance. National Population and Housing Census 2000 http://www.belize.gov.bz/features/cso/ |
Bolivia
| Spatial data | Population data |
|---|---|
| Instituto Geográfico Militar. Mapa de la República de Bolivia. Escala 1:1500000. Proyección Cónica Comforme de Lambert. | Instituto Nacional de estadística, INE. Indicadores Socio-demográficospor Provincias. Censo de 1992. La Paz, Bolivia |
Brazil
| Spatial data | Population data |
|---|---|
| CD-Rom from IGBP | Instituto Brasileiro de Geografia y Estatística, IBGE.Censo Demográfico 2000 |
Cayman Islands
| Spatial data | Population data |
|---|---|
| Digital Chart of the World | Cayman Census, 1989 http://www.columbiagazetteer.org/ and Cayman Census, 1999 http://www.caymanislands.ky/tour_guide/population.asp |
Chile
| Spatial data | Population data |
|---|---|
| Instituto Nacional de Estadísticas. Sub. Depto. Cartografía. Dpto. Geografía y Censos. 1981. Con la nueva Diivisón Política. Escala 1:3000000 and Mapa Caminero Geografico y turistico de Chile Inupal. 1987. Escala 1: 1.400.000 Codigo Ciat 782 gbbg 1989 - 782 fb 198; prepared by CIAT. | Instituto Nacional de Estadisctica, INE. 1992 and 2002; http://www.ine.cl; refinements made at CIESIN using http://www.ine.cl/cd2002/index.php, an intercative map showing 1992 and 2002 population by municipio |
Colombia
| Spatial data | Population data |
|---|---|
| Instituto Geográfico "Agustín Codazzi". 1995. Mapa digitalizado por el DANE. Plancha 1:500000 | Departamento Administrativo Nacional de Estadística, DANE."República de Colombia: Panorama Colombiano." http://www.sin.com.co/clientes/DANE/censo93.html |
Costa Rica
| Spatial data | Population data |
|---|---|
| Instituto Geográfico Nacional. 1984. Mapa de Provincias y Cantones. Escala 1:1500000 | Dirección General de Estadística y Censos. 1996. Instituto Nacional de Estadística y Censos, INEC. IX Censo Nacional de Población y Vivivenda del 2000. http://www.meic.go.cr/. |
Cuba
| Spatial data | Population data |
|---|---|
| Cuba Político administrativo. Escala: 1:1250000. Proyección sin información . Editado en 1997. | Population for 1991 from Census of Cuba 1991 - digital data from
the UN Statistics Division's Software Development Project. Population 2000 came from the Anuario Estadistico de Cuba 2000 from the Oficina Nacional de Estadisticas. |
Dominica
| Spatial data | Population data |
|---|---|
| Digital Chart of the World | Commonwealth of Dominica. Demographic Statistics, No.2, 1996. Central Statistical Office, Ministry of Finance. Roseau, Dominica. |
Dominican Republic
| Spatial data | Population data |
|---|---|
| Mapa de la República Dominicana. Confeccionado por el Instituto Geográfico Universitario. 1985. Escala 1:600000. | 2002 population data obtained from Dominican Republic National Office
of Statistics Census for 2002 http://www.one.gov.do/datos2002.htm,
i.e., Oficina Nacional de Estadísticas, VIII Censo Nacional de Población
y Vivienda 2002, (Resultados Preliminares). 1993 population data from: CENSOS NACIONAL DE POBLACIO Y VIVIENDA 1993 http://www.one.gov.do/datos.htm |
Ecuador
| Spatial data | Population data |
|---|---|
| Instituto Nacional de Estadística y Censos. Divisón Político Administrativa
de la República del Ecuador. 1993. Planchas y escalas: Provincia de Sucumbios 1:250000 Provincia de Napo 1:250000 Provincia de Pastaza 1:250000 Prov. de Morona Santiago 1:250000 Prov. de Zamora Chinchipe 1:250000 Prov. de Esmeraldas 1:250000 Prov. de Manabi 1:250000 Prov. de Los Ríos 1:250000 Prov. de Guayas 1:250000 Prov. El Oro 1:250000 Prov. de Galápagos 1:500000 Prov. de Carchi 1:250000 Prov. de Imbabura 1:250000 Prov. de Pichincha 1:250000 Prov. de Cotopaxi 1:250000 Prov. de Tungurahua 1:250000 Prov. de Bolívar 1:250000 Prov. de Chimborazo 1:250000 Prov. de Canar 1:250000 Prov. de Azuay 1:250000 Prov. de Loja 1:250000 |
Instituto Nacional de Estadística y Censos, INEC. 1990 |
El Salvador
| Spatial data | Population data |
|---|---|
| Dirección General de Estadística y Censos, Unidad de Cartografía 1987. Mapa de la República de El Salvador, División Político-Administrativa. Copia Heliográfica. Escala 1:200000 | Dirección General de Estadística y Censos. 1992. |
Guatemala
| Spatial data | Population data |
|---|---|
| Mapa de la Regionalización de la República de Guatemala. Ministerio de Agricultura. Escala 1:750000. Copia Heliográfica | 1994 population from: Instituto Nacional de Estadística, INE. 1996.
República de Guatemala. Características Generales de Población y Habitación.
Guatemala. 2002 population from: Republica de Guatemala. Instituto Nacional de Estadistica. Censo Nacionales XI de Poblacion y VI de Habitacion 2002, http://www.censos.gob.gt/ |
Guyana
| Spatial data | Population data |
|---|---|
| Guyana North-East Sheet compiled in the Cartographic Division. Lands Department, Ministry of Agriculture | Bureau of Statistics. 1991 |
French Guyana
| Spatial data | Population data |
|---|---|
| Institute Geographique National.Carte Touristique Guyane au 1:500000. 1995 | Institute National de la Statistique et des Etudes Economiques, INSEE, 1995. Tableux Economiques Régionaux. Guyane, 1995, and 1999; http://www.recensement.insee.fr. |
Haiti
| Spatial data | Population data |
|---|---|
| Boundary data sources: (Información digital) Chemonics International 1998. | Institut Haitien de Statistique et de Informatique, IHSI. 1997. |
Honduras
| Spatial data | Population data |
|---|---|
| SERNA, Honduras | 1988 population from Dirección General de Estadística y Censos. 1988.
2001 population from Censo Nacional de Poblacion y Vivienda 2001, Instituto Nacional de Estadistica, downloaded from http://www.ine-hn.org/ |
Jamaica
| Spatial data | Population data |
|---|---|
| Jamaica. Published by the Survey Department, Jamaica Government 1982. Escala 1:250000. | The Statistical Institute of Jamaica, 1991. Population Census 2001 Jamaica Vol 1 Country Report and Preliminary Report for 1991's Urban /Rural |
Mexico
| Spatial data | Population data |
|---|---|
| Mapa Geoestadístico. Secretaría de Programación y Presupuesto (S.P.P.). 1981. Escala 1:1000000 con información del X Censo de Población y Vivienda de 1980. 4 hojas: Norte, Centro, Noroeste y Sudeste. | 1990 and 2000 municipio data downloaded from SIMBAD, 28 April 2004 (Toda la Base de Datos Municipal INEGI from http://www.inegi.gob.mx/inegi/default.asp). |
Nicaragua
| Spatial data | Population data |
|---|---|
| Mapa de la División Político Administrativa, 1997. Proyección Transversal de Mercator. Escala: 1:750000 | Instituto Nacional de Estadística y Censos, INEI.1996. Censos Nacionales 1995, Cifras Oficiales finales. Managua, Nicaragua. |
Panama
| Spatial data | Population data |
|---|---|
| República de Panamá. Mapa Político. Instituto Geográfico Nacional "TOMMY GUARDIA". 1998. Escala: 1:1000000 | Dirección de Estadística y Censos, DEC. X Censo Nacional de Población
y VI de Vivienda 2000. http://contraloria.gob.pa/
Direccion de Estadistica y Censo Censos nacionales de Poblacion Y Vivienda 13 Mayo de 1990 Cifras Preliminarios Junio de 1990 |
Paraguay
| Spatial data | Population data |
|---|---|
| Dirección General de Estadística, Encuesta y Censos. FNUAP-PNUD.
1995. Atlas de Necesidades Básicas Insatisfechas del Paraguay. Planchas
y escalas: Dpto. Canindeyu 1:700000 Dpto. Amambay 1:850000 Dpto. Neembucu 1:750000 Dpto. Central 1:400000 Dpto. Paraguari 1:600000 Dpto. Misiones 1:600000 Dpto. Itapua 1:900000 Dpto. Caazapa 1:650000 Dpto. Alto Paraná 1:800000 Dpto. Caaguazu 1:800000 Dpto. Guaira 1:420000 Dpto. Cordillera 1:400000 Dpto. San Pedro 1:800000 Dpto. Concepción 1:750000 Dpto. Occidental 1:300000 |
Dirección Nacional de Estadística, Encuestas y Censos, DGEEC, 1995.
Atlas del Paraguay 1995. Necesidades Básicas Insatisfechas, Asunción,
Paraguay. Dirección General de Estadística, Encuestas y Censos, 2002. |
Peru
| Spatial data | Population data |
|---|---|
| Instituto Geográfico Nacional. 1984. Mapa Físico Político del Perú. Proyección Mercator Transversa. Escala: 1:1000000. 4 hojas. | Instituto Nacional de Estadística e Informática, INEI. "Población nominalmente censada, por áreas urbana y rural y sexo, según Provincia y Distrito: 1993" http://contraloria.gob.pa/ |
Puerto Rico
| Spatial data | Population data |
|---|---|
| US Census Bureau | US Census Bureau: 1990 Decennial Census and 1997 Population Estimates |
Surinam
| Spatial data | Population data |
|---|---|
| 1- Distrikt Nickerie 1:300000 Hoja C.B.L. 469-1 2- Distrikt Coronie 1:200000 Hoja C.B.L. 469-2 3- Distrikt Saramacca 1:200000 Hoja C.B.L. 469-3 4- Distrikt Wanica 1:50000 Hoja C.B.L. 469-4 5- Distrikt Commewijne 1:200000 Hoja C.B.L. 469-6 6- Distrikt Marowijne 1:200000 Hoja C.B.L. 469-7 7- Distrikt Para 1:200000 Hoja C.B.L. 469-8 8- Distrikt Paramaribo 1:25000 Hoja C.B.L. 469-5 9- Distrikt Brokopondo 1:200000 Hoja C.B.L. 469-9 10- Distrikt Sipaliwini 1:1000000 Hoja C.B.L. 469-10Q |
General Bureau of Statistics, 1999 |
Trinidad and Tobago
| Spatial data | Population data |
|---|---|
| Republic of Trinidad and Tobago Central Statistical Office (CSO), 1988. | Ward level data for 1990, Central Statistical Office, 1990 Population
and Housing Census, Vol II(2), Demographic Report, 1994 Port of Spain.
The 1990 county and 2000 county and wards within St George County obtained from the Trinidad and Tobago Central Statistics Office 2000 Census Table 8 http://www.cso.gov.tt/statistics/cssp/census2000/default.asp. |
Uruguay
| Spatial data | Population data |
|---|---|
| Servicio Geográfico Militar. 1992. Mapa de la República Oriental del Uruguay, carta geográfica división política. Escala: 1:500000 Prepared by CIAT. | Instituto Nacional de Estadística, INE, 1994. Anuario Estadístico. Montevideo, Uruguay. |
Venezuela
| Spatial data | Population data |
|---|---|
| Oficina Central de Estadística e Informática Presidencia de la República. Dirección de Geografía y Cartografía. 1993. Mapa de la División Política Territorial de Venezuela. Copia Heliográfica. | Oficina Central de Estadística e Informática, OCEI, 1991. Tiempo
de resultados, primeros resultados Censo 1990. Caracas, Venezuela. Instituto Nacional de Estadística, Republica Bolivariana de Venezuela. XIII Censos General de Poblacio y Vivienda, Primeros Resultados, Censo 2001. Downloaded from http://www.ine.gov.ve/ine/censo/fichascenso/fichacenso.asp |
A.5. Map of administrative units in Latin America and the Caribbean
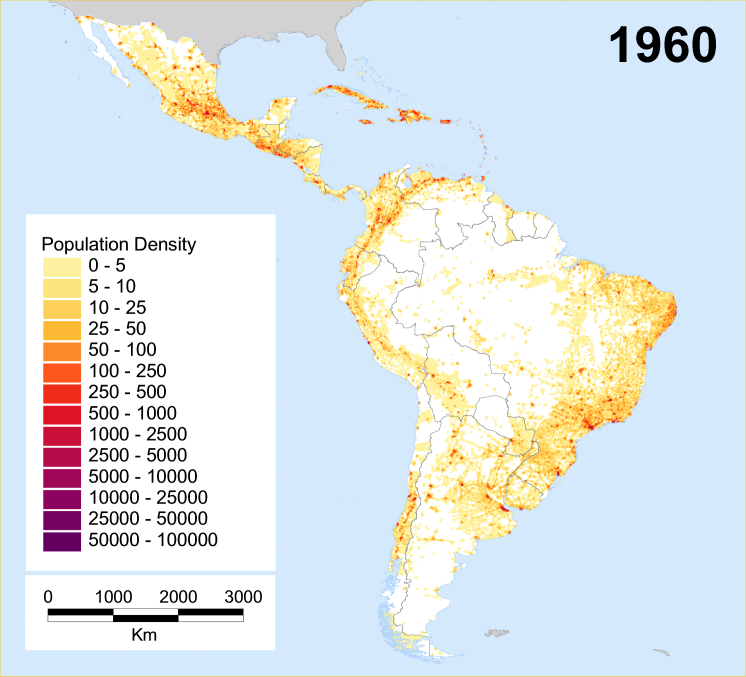
A.6. Population density map for years [ 1960 | 1970 | 1980 | 1990 | 2000 ]
A.7. Roads used in the accessibility model
A.8. Populated places used in the accessibility model*
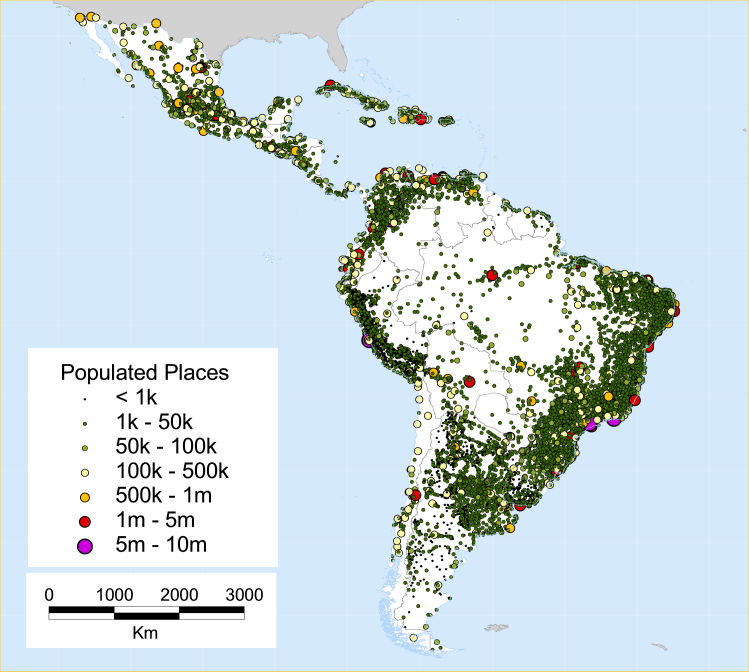
* Populated places from Center for International Earth Science Information Network (CIESIN), Columbia University; International Food Policy Research Institute (IPFRI), the World Bank; and Centro Internacional de Agricultura Tropical (CIAT), (2004) Global Rural-Urban Mapping Project (GRUMP): Gridded Population of the World, version 3, with Urban Reallocation (GPW-UR). Palisades, NY: CIESIN, Columbia University.
Acknowledgments
The International Center for Tropical Agriculture (CIAT) supported the development of administrative and population databases for Latin America and the Caribbean through their Geographic Information Systems laboratory and the Land Use project. Silvia Elena Castaño, Rosalba Lopez, Alexander Cuero, Carlos Nagles, Elizabeth Barona and Peter Jones developed many of the foundation data sets used in this project. We thank Liliana Perez for her work to verify the quality of the database. We are grateful for the cooperation of the United Nations Economic Commission for Latin America (ECLAC), the World Bank and all the countries of Latin America and the Caribbean that supported this effort. This version of the database was made in close cooperation with the Center for International Earth Science Information Network’s (CIESIN) Gridded Population of the World, Version 3 project. The The Inter-American Development Bank (IADB), United Nations Environment Program (UNEP/GRID Sioux Falls , UNEP/GRID Arendal), the World Resources Institute (WRI), and the International Food Policy Research Institute (IFPRI) provided funding and support throughout the development of this project.